Tree based algorithms are among the most common and best supervised Machine Learning algorithms. Decision Trees follow a human-like decision making approach by breaking the decision problem into many smaller decisions. As opposed to black-box models like SVM and Neural Networks, Decision Trees can be represented visually and are easy to interpret.
How is decision making represented as a tree?
Let’s consider a very basic example. Suppose you want to classify customers as buyers and non-buyers and that your decision criteria is based on the following attributes/features: UserStatus, NumberOfProductsViewed, IsEveningVisitor, HasProductsInBasket and VisitDuration. If we phrase these features as questions — UserStatus as “Is the User known?” — a simple decision making process could be represented as:

So the basic idea is that at each point we consider a set of questions that can partition our dataset. We choose the question (User is known? Yes/No) that allows us to best split the group into two categories (buyers and non-buyers) and then find again the new best questions for the new partitions (Views more than 3 products? Visits in the evenings? Yes/No). We stop once all the points after the split are of the same class (all buyers or all non-buyers). Once we have created our tree model, these questions will act as a guide in assigning the appropriate class for an unknown datapoint (new user) — drop the new datapoint down the tree and get the label assigned by the last question.
A decision tree is represented upside down. The first node is termed as root node. The most important feature occurs at the top — UserStatus is more important than VisitDuration. In the image above, the boxes/internal nodes represent the condition based on which the tree splits into branches/edges. The end of the branch that doesn’t split anymore is called terminal/leaf node — in this case, whether the customer is a buyer or not.
The above tree is called a Classification tree as the outcome is binary — buyer or non-buyer. Regression trees are also represented in the same manner; they just predict continuous values like income of a person or price of a house. Commonly, Decision Tree algorithms are referred to as CART or Classification and Regression Trees.
Pseudocode for the Decision Tree Algorithm
- Assign the best feature/attribute from the dataset to the root node.
- Split the training set into subsets such that each subset contains data with the same value for an attribute. For example, if the feature is NumberOfProductsViewed then subset1 will consist of users who have viewed more than 3 products while subset2 will be users who have viewed <= 3 products.
- Repeat step 1 and step 2 on each subset until you find leaf nodes in all the branches of the tree.
Note: A popular Python library for implementing Decision Trees is Scikit-Learn. Scikit-Learn provides an easy to use api — you will have a model up and running with just a few lines of code in python!
How does a tree decide where to split, which attributes/features to use?
If we have a dataset consisting of N attributes and we want to decide which attribute to place as root node or at different levels of the tree as internal nodes, then we require some smartness — randomly selecting nodes would generally give bad results with low accuracy. The process of identifying the right features for each node is known as Attributes Selection.
There exist different measures to identify which attribute to consider as the root node at each split. The two most popular attribute selection measures are:
- Gini index – for categorical attributes e.g., gender
- Information gain – for continuous attributes e.g., salary
These criterions calculate a measure (some values) for every attribute and the attribute with the best measure is selected at each split— in case of information gain, the attribute with highest value will be selected as root node.
Note: In a practical scenario, you will NOT have to worry about calculating these measures yourself! The explanation below is just for understanding what is going under the hood.
Gini Index
A Gini score gives an idea of how good a split is by how mixed the response classes are in the groups created by the split.
Let’s see this with our example: our target variable is a binary variable (buyer and non-buyer). If we represent buyer with 1 and non-buyer with 0, there can be 4 combinations of actual and predicted outcome (1|1; 1|0; 0|1; 0|0):
P(Class=1).P(Class=1) + P(Class=1).P(Class=0) + P(Class=0).P(Class=1) + P(Class=0).P(Class=0) = 1
P(Class=1).P(Class=0) + P(Class=0).P(Class=1) = 1 – P2(Class=0) – P2(Class=1)
Gini Index for Binary Target variable is: 1 – P2(Class=0) – P2(Class=1)
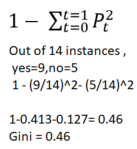
Simply put, the Gini index is just the probability of obtaining two different outputs. Minimum value of Gini Index will be 0 when all observations belong to one class/label (a perfect separation of results), whereas a worst case split results in 50/50 classes.
Information Gain
By using information gain as a criterion, we estimate the information provided by each attribute. We take some help from information theory here. Information theory gives us a measure to define the degree of disorganization in a system known as Entropy.
For a binary classification problem:.
- If all examples are positive or all are negative — homogeneous sample — then entropy will be zero (a partition resulting in a group with only buyers or non-buyers)
- If the samples are equally divided into positive and negative classes then entropy will be one (50% buyers and 50% non-buyers)
Entropy can be calculated as follows:
![]()
For example, if we have 14 users and 9 are classified as buyers and 5 as non-buyers:
H(X) = -9/14*log2(9/14) – 5/14*log2(5/14) = 0.41 + 0.53 = 0.94
Calculating entropy measures for each attribute allows us to derive Information Gain as 1 – Entropy.
The difference in entropy before and after splitting a branch, based on a given attribute, gives us the quality of the split. And the goal is to find attributes that returns the highest information gain (i.e., the most homogeneous branches).
When to stop growing a tree?
A large number of features results in a large number of splits and a huge tree. A huge tree would be computationally expensive, difficult to interpret and would probably not work very well with new data — problem called overfitting. However, if splitting is stopped too early, we loose on performance. So when to stop?
Some common stopping criteria:
- Number of cases in the leaf node is less than some prespecified minimum. For example, we can use a minimum of 10 users to reach a decision (buyer or non-buyer) and discard any leaves with less than 10 users.
- Depth of the tree has reached a prespecified maximum depth (length of the longest path from root to a leaf).
- Continue splitting until error on validation set is minimum
- Trade off between tree complexity or size vs. test set accuracy
Pruning
While stopping criteria are a relatively crude method of stopping tree growth, an alternative approach is to allow the tree to grow and then prune it back to an optimum size. Pruning involves removing branches that use features having low importance or, in other words, removing the parts of the tree which add very little to the predictive power of the tree. This reduces both complexity and overfitting.
The simplest forms of pruning is reduced error pruning: starting at the leaves, each node is replaced with its most popular class (e.g., for a split that results in 8 buyers and 2 non-buyers, we mark the outcome as buyer). If the prediction accuracy does not deteriorate then the change is kept.
Advantages of Decision Trees
- Easy to understand, interpret and visualize.
- Provide feature selection – easy and fast way to identify most significant features.
- Can handle both classification and regression problems.
- Can handle non-linear relationships between variables.
Disadvantages of Decision Trees
- Overfitting: over-complex trees that do not generalize the data well.
- Unstable: small variations in the data can result in a completely different tree. This is called variance and it can be lowered by methods called bagging and boosting.
- No guarantee of a globally optimal decision tree. This issue can be mitigated by using Random Forests. In Random Forests, we train multiple trees as opposed to a single tree in CART. In this case, the features and instances are randomly sampled with replacement.
End Notes
By now you should have a good understanding of the basics of Decision Trees. In the next post, we will see a practical end-to-end example using Scikit-Learn.
Did you find this post useful? Feel free to share suggestions and opinions in the comments section below. For continuing your journey Towards Machine Learning, and to stay up-to-date with the latest posts, you can leave your email. Thanks for reading! 🙂
